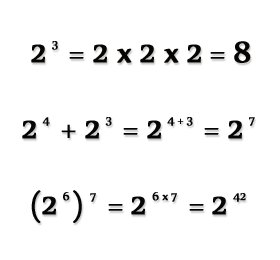Bibliografias

http://www.educar.org/enlared/planes/paginas/funcionexponencial.htm
http://facultad.bayamon.inter.edu/ntoro/expow.htm
http://www.rmm.cl/index_sub.php?id_contenido=11186&id_seccion=3359&id_portal=509

Leyes de los exponentes

Funciones Logaritmicas

Definición:

El logaritmo de un número y en el exponente al cual hay que elevar la base b para obtener a y. Esto es,  si  b > 0  y   b  es  diferente  de  cero,   entonces log_b y = x  si y sólo si  y = b^x.

La notación log_b y = x se lee “el logaritmo de y en la base b es x”.

Las inversas de las funciones exponenciales se llaman funciones logarítmicas. Como la notación f ¹ se utiliza para denotar una función inversa, entonces se utiliza otra notación para este tipo de inversas.  Sif(x)= b^x, en lugar de usar la notación f^-1(x), se escribe log_b (x) para la inversa de la función con base b. Leemos la notación log_b(x) como el “logaritmo de x con base b”, y llamamos a la expresión log_b(x) un logaritmo.

Gráficas de funciones logarítmicas:

 Las funciones y= b^x  y  y = log_b x  para b>0  y  b diferente de uno son funciones inversas.  Así que la gráfica de  y = log_b x es una reflexión sobre la recta y = x de la gráfica  de  y = b^x.  La gráfica de y = b^x tiene como asíntota horizontal al eje de x  mientras  que la gráfica de  y = log_b x tiene al eje de y como asíntota vertical.

Ejemplo:

Las funciones y = 2^x   y y = log₂ x son funciones inversas una de la otra, por tanto, la gráfica de y = log₂ x es una reflexión de la gráfica de y = 2^x sobre la recta y=x. El dominio de y=2^x es el conjunto de los números reales y el recorrido es todos los números reales mayores que cero.  El dominio de y=log₂ x es el conjunto de los números reales mayores que cero y el recorrido el conjunto de los números reales.

Rango y Dominio

El rango

El rango sólo se produce en el ámbito de la función de los valores de X, por lo que a fin de determinar el rango de una función, usted necesita primero saber determinar el dominio de la función. En otras palabras, el rango de una función es el conjunto de valores que se obtiene cuando se conectan los valores de X en el dominio de dicha función dentro de la función y resolver para Y.

Ejemplo 1:

y= 3x+2

Entonces lo primero que hacemos es despejar a “x” en términos de “y” vamos que la función adquiere la siguiente forma:

x= (y-2)/3,

Vemos que en esta relación la “y” puede tomar cualquier valor en el conjunto de los reales por lo que decimos que el rango de la función son todos los valores pertenecientes al conjunto de los reales ,que es lo mismo que decir que el rango de la función son todos los números del intervalo entonces:

Rango: (-∞, ∞)

Ejemplo 2:

y=1/x,

x=1/y

Como podemos ver en esta relación la “y” no puede tomar el valor de cero ya que habría una indeterminación por lo que no podemos decir que el rango de la función sea todo el conjunto de los reales, entonces decimos que el rango de esta función son todos los reales exceptuando al valor de cero.

Rango: (-∞,0) (0, ∞)

                           

dominio

DOMINIO DE UNA FUNCIÓN: ES EL CONJUNTO FORMADO POR LOS

ELEMENTOS QUE TIENEN IMAGEN. LOS VALORES QUE LE DAMOS A “X” (VARIABLE INDEPENDIENTE) FORMAN EL CONJUNTO DE PARTIDA. GRÁFICAMENTE LO MIRAMOS EN EL EJE HORIZONTAL (ABSCISAS), LEYENDO COMO ESCRIBIMOS DE IZQUIERDA A DERECHA.

EL DOMINIO DE UNA FUNCIÓN ESTÁ FORMADO POR AQUELLOS VALORES DE “X”

(NÚMEROS REALES) PARA LOS QUE SE PUEDE CALCULAR LA IMAGEN F(X)eN LA GRÁFICA ANTERIOR NOTAMOS QUE SI LE ASIGNAMOS LOS VALORES “-2” Y “-1” A LA “X” ESTOS NO TIENEN IMAGEN, POR LO TANTO NO PERTENECEN AL DOMINIO DE LA FUNCIÓN ESTUDIADA. ESTO ES LÓGICO YA QUE LOS NÚMEROS NEGATIVOS NO TIENEN RAÍCES REALES SINO RAÍCES IMAGINARIAS.

Funciones Exponenciales

Una función exponencial es aquella en la que la variable está en el exponente.  Se expresa de la forma   en donde a es un número real, positivo y diferente a 1 (a>0, a≠1).  La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque funciones de la forma f(x)= no tendrían sentido en los números reales

 Como ejemplo de estas tenemos: 

y= 2x

y= 45x

y= 10x-3

y= 82x+1 

Aplicaciones de las funciones logarítmicas

Cuando se habla de logaritmos, seguramente muchas personas creen que no sirven para nada más que para ser resueltas en clase y nada más, esta información que veremos.

Los logaritmos son números, que se descubrieron para facilitar la solución de los problemas aritméticos y geométricos, a través de esto se evitan todas las complejas multiplicaciones y divisiones transformándolo a algo completamente simple a través de la substitución de la multiplicación por la adición y la división por la sustracción. Además el cálculo de las raíces se realiza también con gran facilidad

Algunas de las utilidades son:

• En la Economía y la Banca: Los índices de crecimiento son exponenciales, se aplica en la demanda y oferta, así como obtener los porcentajes de los parámetros. Mientras en la banca sirve para medir el crecimiento de los depósitos de acuerdo al tiempo.

• En la Estadística: Suele aplicarse en el crecimiento de la población.

• En la Publicidad: Cuando se realizan las estadísticas sobre la campaña publicitaria que se va a lanzar, se realizan cálculos matemáticos con logaritmos. Estas estadísticas definen el fracaso o éxito de la campaña.

• En la Medicina: Solo es aplicable en ciertos fenómenos tales como el resultado del experimento psicológico de Stenberg. También se aplica en la inmunología.

• En la Psicología: Se utiliza en la ley de Weber-Fechner, fenómeno del estimulo y respuesta. Aquí la respuesta (R) se relaciona con el estimulo (E) mediante una ecuación donde por ejemplo E0 es el valor mínimo del estimulo que se encuentra en el sujeto.

• En la Biología: Es aplicado en los estudios de los efectos nutricionales de los organismos. Así como también en el cálculo del PH. También en la genética, donde se utiliza la estadística y la probabilidad para saber sobre lo que un hijo heredara de sus padres.

• En la Geología: Sirven de cálculo para calcular la intensidad de un evento, así como un sismo o un terremoto. Aquí es usado en la escala de Richter,donde la intensidad de un sismo se conoce en base a los logaritmos. 

• En la Ingeniería Civil: Cuando se resuelven problemas específicos, siempre teniendo en cuenta una ecuación de segundo grado.

• En la Astronomía: Para determinar la magnitud estelar de una estrella o planeta se usan cálculos de carácter logarítmico para determinar la brillantez y magnitud.  Al establecer la luminosidad visible de una estrella, se opera con tablas de logaritmos en base 2.5.

• En la Música: El pentagrama es una escala logarítmica ya que la altura del sonido es proporcional  a la del número de frecuencia, además ayuda a medir los grados de tonalidad ya que se pueden representar por el logaritmo en base 2.

• En la Topografía: Cuando queremos determinar la altura de un edificio usando la base y el ángulo.

• En la Química: Para calcular el PH de las sustancias se utilizan logaritmos. El PH normalmente es medido constantemente debido al efecto de las lluvias ácidas producidas por el azufre de las plantas eléctricas y fabricas.

• Uno de los casos importantes de la aplicación de logaritmos aparte de la astronomía y las demás ciencias, creo que hay que resaltar el uso de logaritmos en la música.

Duran Vázquez Karina

Monroy Velázquez Alejandra

Santos Ramírez Carlos 

Funciones en la vida cotidiana

Se llaman ecuaciones exponenciales a las ecuaciones en las que en algún miembro aparece una expresión exponencial (potencia de base constante (número) y exponente variable (x, y, etc.).

Las ecuación exponenciales se definen como: f(x)=ax donde la base a es un número real cualquiera positivo y distinto de 1.

Usos:

 • Desde el punto de vista de la matemática de un hecho o fenómeno del mundo real, las ecuaciones exponenciales se usan desde el tamaño de la población hasta fenómenos físicos como la aceleración, velocidad y densidad.

 • Se usan igual para dar el crecimiento de cosas como: el crecimiento de una población determinada, el crecimiento de personas infectadas con el VIH (sida), o la disminución de una carga de la carga de un condensador, inundaciones de tiendas agrícolas, vida media de una sustancia radioactiva, desintegración atomiza, etc.

 • Ha sido utilizada para obtener el área, el volumen, de cuerpos geométricos, además se usa en el dimensionamiento de envases para productos líquidos (leche, agua) y productos granulados como (arroz, detergente, leche en polvo) etc. Y resuelven problemas de desarrollo y descomposición.

Áreas Científicas:

Ø  Demografía

Ø  Biología

Ø  Matemáticas

Ø  Física

Ø  Química

Ø  Área Farmacéutica

Ejemplos:

APLICACIÓN EN ECONOMÍA

Se calcula que el monto del capital, en millones de pesos, que tiene depositado un señor en el banco, en cualquier momento (t) meses puede ser calculado mediante la función f (t) = 7,5. 1,02t.
Función: C = C0 (½) kt, donde C0 es la cantidad inicial de carbono, t es.
El número de años  que pasan. Si la vida media del carbono 14 es 5730 años.

APLICACIONES EN LA VIDA INVESTIGACIONES  POLICIALES:

Una persona es encontrada Muerta en su Departamento, la Brigada de Homicidios llego a las 10 de la noche, los datos recogidos por los Detectives fueron temperatura de la habitación 21ºC (A) ,  la temperatura del cadáver al ser encontrado fue de 29ºC y una hora después era   28ºC .Considerando la función: T(t) = A + (B – A ) e ^–kt
Calcular el valor de K si t = 1
Con el dato anterior Determine la hora en que fue encontrado el cuerpo inerte si este tenía una temperatura de 37ºC cuando estaba vivo.

APLICACIONES EN BIOLOGÍA:

-Para ver la expansión de criaturas.
-Como se reproducen las bacterias en segundos minutos horas etc.
-La progresión de enfermedades en el cuerpo.
-El aumento o disminución de glóbulos e la sangre.

Ejemplo de aplicación:

Una población de bacterias que se duplica cada 20 minutos; la población mundial que crece al1.14% (unas 75 millones de personas por año); el valor de un coche que se deprecia 10% anual; un virus muy infeccioso como el SARS o la viruela (cada enfermo infecta a varios); un depósito en el banco que aumenta al 5% anual; una substancia radiactiva que se descompone (en este caso la cantidad presente disminuye exponencialmente) : todos ellos y muchos más son ejemplos de funciones exponenciales o procesos que pueden interpretarse como funciones exponenciales.

Tiempo de Duplicación.

Una forma rápida de calcular el tiempo de duplicación (de un depósito bancario a interés compuesto, o de una población) en una función exponencial es aplicar la muy antigua Regladle 70, (o del 72, también llamada) que ya descubrió en la Edad Media el monje Luca Pacioli, el sabio que inventó la contabilidad: 70/r

Si tenemos que la población mundial crece al r= 1,14 % anual, dividimos 70/1,14 = 61,40 años.

La población mundial, actualmente, se duplica en algo más de 61 años.

En 1963 el crecimiento de la población mundial era la escalofriante proporción de r = 2,20 %por año. Vemos si había diferencia en el tiempo de duplicación.

70/2,20 = 31,8 años

INTERÉS COMPUESTO

La función exponencial aparece ligada en el cálculo de intereses compuestos.
Recordemos que el interés compuesto es aquél donde el interés generado por un capital es reinvertido de modo que en el siguiente período éste genera también intereses.
Suponga P, el cual llamaremos monto principal, principal o capital inicial, es invertido a una tasa simple de t por periodo, entonces el interés final al cabo del periodo de interés es Pt, teniendo como capital al final de este periodo: P + tP = P (1+ t). Si esta cantidad es reinvertida a la misma tasa, el interés generado será de P (1+ t) t y ahora en este segundo periodo el nuevo principal será de  P (1+ t) + P (1+ t) t = P (1+ t) (1+ t) = P (1+ t)².

Podemos chequear que el principal al finalizar el tercer periodo será de P (1+ t)³.
Más generalmente, al finalizar el periodo k, el monto acumulado A o monto total o capital final será de: k A = P (1+ t) ^k

Donde t es la tasa de interés por periodo y P el capital inicial.
El interés compuesto es la diferencia entre el monto acumulado y el monto inicial (Capital final menos capital inicial).

CRECIMIENTO Y DECRECIMIENTO POBLACIONAL

Supongamos que el tamaño inicial de una población es P₀, y la población aumenta a una tasa por periodo de r, al finalizar un periodo de tiempo la población habrá aumentado P₀r y el tamaño total de la población al final de este periodo será de: P₀ + rP₀ = P₀ (1 + r). 

En un segundo periodo de tiempo la población aumentará a una tasa de r sobre una población de P₀ (1 + r), entonces el aumento de la población en el segundo periodo de tiempo es de P₀ (1+ r) r  y ahora, al finalizar este segundo periodo de tiempo, el tamaño de la población será de:
 

P₀ (1+ r) + P₀ (1+ r)r = P₀(1 + r) +(1+ r) = P₀ (1+ r)².
Podemos chequear que el tamaño de la población al finalizar el tercer período será de:

P₀ (1+ r)³.
Más generalmente, al finalizar el periodo t, el tamaño de la población P (t) será:

P (t)= P₀ (1+ r) ^t.
Donde P₀ es el tamaño inicial de la población.

¿Que es una Función Exponencial?

Una función exponencial es aquella en la que la variable está en el exponente.  Se expresa de la forma   en donde a es un número real, positivo y diferente a 1 (a>0, a≠1).  La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque funciones de la forma f(x)= no tendrían sentido en los números reales. Es una función con una base constante elevada a una variable.  Estas funciones tienen gran aplicación en campos muy diversos como la biología, administración, economía, química, física e ingeniería..

La definición de función exponencial exige que la base sea siempre positiva y diferente de uno (b>0 y b≠1). La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque no tendrían sentido en los números reales.

Funciones:

1) f(x) = 2^x

x	-3	-2	-1	0	1	2	3
	f(x)	1/8	1/4	1/2	1	2	4	8

 

¿Que es un exponente?

En el campo de las matemáticas, se conoce como potenciación a la operación que implica una serie de multiplicaciones de un número dado una cantidad de veces determinada; el primer componente se denomina base y se representa con la letra a, mientras que el segundo se llama exponente y se escribe como una n. En este caso, un exponente es una expresión algebraica o un simple número que denota la potencia a que se debe elevar otra expresión u otro número (la base).

El exponente se debe colocar en la parte superior derecha del elemento que se desea elevar. La forma de leer una operación de este tipo es “a elevado a n“, aunque también puede decirse “a elevado a la n“. Por otro lado, es importante señalar que en el caso de los exponentes 2 y 3, las correctas lecturas son “a elevado al cuadrado” y “a elevado al cubo“, respectivamente.

La potenciación suele generar confusiones a las personas ajenas a las matemáticas, pero se trata de una operación muy sencilla, ya que se basa en la multiplicación, la cual, a su vez, parte de la suma. Si tomamos el ejemplo 2 elevado al cubo (o sea, a la tercera potencia), los pasos a seguir son los siguientes: multiplicar a 2 por sí mismo y, luego, el resultado por dos; esto nos da 8.

Dado que nuestro exponente (3) es un número natural, o sea que pertenece al conjunto de números que utilizamos para contar cosas en el mundo real, indica la cantidad de veces que la base (2) aparecerá en una multiplicación donde será el único factor. De este modo, 2 elevado al cubo se convierte en 2 x 2 x 2, que da como resultado 8. De esta nueva representación se puede deducir que 2 elevado a la 1 es 2, y lo mismo ocurre en todos los casos.

Cabe mencionar que cualquier número distinto a 0 que es elevado a 0 da como resultado 1. En cambio, 0 elevado a 0 es un caso particular que no está definido.